Movimiento rectilíneo uniforme
Para este caso, la velocidad del vector se mueve hacia la dirección fornica del lado obstante por lo tanto esto puede decirse que la velocidad se vuelve en cero por lo que la velocidad permanece constante a lo largo del tiempo. Esto corresponde al movimiento de un objeto lanzado en el espacio fuera de toda interacción, o al movimiento de un objeto que se desliza sin fricción. Siendo la velocidad v constante, la posición variará linealmente respecto del tiempo, según la ecuación:
donde  es la posición inicial del móvil respecto al centro de coordenadas, es decir para
es la posición inicial del móvil respecto al centro de coordenadas, es decir para 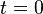 .
.
 es la posición inicial del móvil respecto al centro de coordenadas, es decir para
es la posición inicial del móvil respecto al centro de coordenadas, es decir para 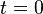 .
.
Si  la ecuación anterior corresponde a una recta que pasa por el origen, en una representación gráfica de la función
la ecuación anterior corresponde a una recta que pasa por el origen, en una representación gráfica de la función  , tal como la mostrada en la figura 1.
, tal como la mostrada en la figura 1.
 la ecuación anterior corresponde a una recta que pasa por el origen, en una representación gráfica de la función
la ecuación anterior corresponde a una recta que pasa por el origen, en una representación gráfica de la función  , tal como la mostrada en la figura 1.
, tal como la mostrada en la figura 1.[editar]Movimiento rectilíneo uniformemente acelerad
En éste movimiento la aceleración es constante, por lo que la velocidad de móvil varía linealmente y la posición cuadráticamente con tiempo. Las ecuaciones que rigen este movimiento son las siguientes:
Donde  es la posición inicial del móvil,
es la posición inicial del móvil,  es la posición final y
es la posición final y 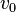 su velocidad inicial, aquella que tiene para
su velocidad inicial, aquella que tiene para 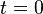 .
.
 es la posición inicial del móvil,
es la posición inicial del móvil,  es la posición final y
es la posición final y 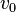 su velocidad inicial, aquella que tiene para
su velocidad inicial, aquella que tiene para 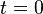 .
.
Obsérvese que si la aceleración fuese nula, las ecuaciones anteriores corresponderían a las de un movimiento rectilíneo uniforme, es decir, con velocidad 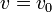 constante.
constante.
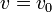 constante.
constante.
Dos casos específicos de MRUA son la caída libre y el tiro vertical. La caída libre es el movimiento de un objeto que cae en dirección al centro de la Tierra con una aceleración equivalente a la aceleración de la gravedad (que en el caso del planeta Tierra al nivel del mar es de aproximadamente 9,8m/s2). El tiro vertical, en cambio, corresponde al de un objeto arrojado en la dirección opuesta al centro de la tierra, ganando altura. En este caso la aceleración de la gravedad, provoca que el objeto vaya perdiendo velocidad, en lugar de ganarla, hasta llegar al estado de reposo; seguidamente, y a partir de allí, comienza un movimiento de caída libre con velocidad inicial nula.
[editar]Movimiento armónico simple
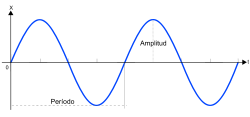
Es un movimiento periódico de vaivén, en el que un cuerpo oscila a un lado y a otro de una posición de equilibrio en una dirección determinada y en intervalos iguales de tiempo. Matemáticamente, la trayectoria recorrida se expresa en función del tiempo usando funciones trigonométricas, que son periódicas. Así por ejemplo, la ecuación de posición respecto del tiempo, para el caso de movimiento en una dimensión es:
ó
Los movimientos del péndulo, de una masa unida a un muelle o la vibración de los átomos en lasredes cristalinas son de estas características.
La aceleración que experimenta el cuerpo es proporcional al desplazamiento del objeto y de dirección contraria, desde el punto de equilibrio. Matemáticamente:
donde  es una constante positiva y
es una constante positiva y  se refiere a la elongación (desplazamiento del cuerpo desde la posición de equilibrio).
se refiere a la elongación (desplazamiento del cuerpo desde la posición de equilibrio).
 es una constante positiva y
es una constante positiva y  se refiere a la elongación (desplazamiento del cuerpo desde la posición de equilibrio).
se refiere a la elongación (desplazamiento del cuerpo desde la posición de equilibrio).
La solución a esa ecuación diferencial lleva a funciones trigonométricas de la forma anterior. Lógicamente, un movimiento periódico oscilatorio real se ralentiza en el tiempo (por fricciónmayormente), por lo que la expresión de la aceleración es más complicada, necesitando agregar nuevos términos relacionados con la fricción. Una buena aproximación a la realidad es el estudio del movimiento oscilatorio amortiguado.
Véase también: Oscilador armónico.
Movimiento parabolico
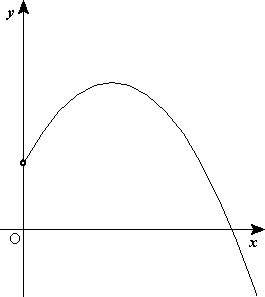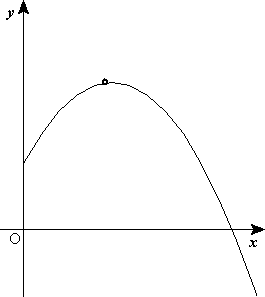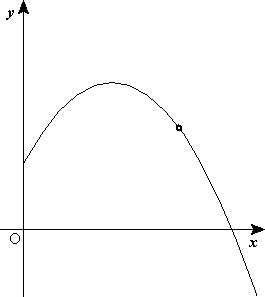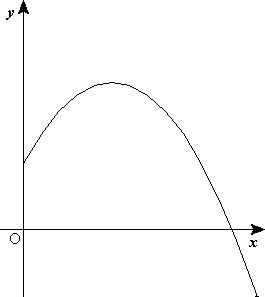
El movimiento parabólico se puede analizar como la composición de dos movimientos rectilíneos distintos: uno horizontal (según el eje x) develocidad constante y otro vertical (según eje y) uniformemente acelerado, con la aceleración gravitatoria; la composición de ambos da como resultado una trayectoria parabólica.
Claramente, la componente horizontal de la velocidad permanece invariable, pero la componente vertical y el ángulo θ cambian en el transcurso del movimiento.
En la figura 4 se observa que el vector velocidad inicial 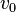 forma un ángulo inicial
forma un ángulo inicial  respecto al eje x; y, como se dijo, para el análisis se descompone en los dos tipos de movimiento mencionados; bajo este análisis, las componentes según x e y de la velocidad inicial serán:
respecto al eje x; y, como se dijo, para el análisis se descompone en los dos tipos de movimiento mencionados; bajo este análisis, las componentes según x e y de la velocidad inicial serán:
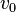 forma un ángulo inicial
forma un ángulo inicial  respecto al eje x; y, como se dijo, para el análisis se descompone en los dos tipos de movimiento mencionados; bajo este análisis, las componentes según x e y de la velocidad inicial serán:
respecto al eje x; y, como se dijo, para el análisis se descompone en los dos tipos de movimiento mencionados; bajo este análisis, las componentes según x e y de la velocidad inicial serán:
El desplazamiento horizontal está dado por la ley del movimiento uniforme, por tanto sus ecuaciones serán (si se considera  ):
):
 ):
):
En tanto que el movimiento según el eje 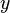 será rectilíneo uniformemente acelerado, siendo sus ecuaciones:
será rectilíneo uniformemente acelerado, siendo sus ecuaciones:
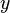 será rectilíneo uniformemente acelerado, siendo sus ecuaciones:
será rectilíneo uniformemente acelerado, siendo sus ecuaciones:
Si se reemplaza y opera para eliminar el tiempo, con las ecuaciones que dan las posiciones  e
e 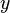 , se obtiene la ecuación de la trayectoria en el plano xy:
, se obtiene la ecuación de la trayectoria en el plano xy:
 e
e 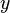 , se obtiene la ecuación de la trayectoria en el plano xy:
, se obtiene la ecuación de la trayectoria en el plano xy:
que tiene la forma general
y representa una parábola en el plano y(x). En la figura 4 se muestra esta representación, pero en ella se ha considerado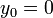 (no así en la animación respectiva). En esa figura también se observa que la altura máxima en la trayectoria parabólica se producirá en H, cuando la componente vertical de la velocidad
(no así en la animación respectiva). En esa figura también se observa que la altura máxima en la trayectoria parabólica se producirá en H, cuando la componente vertical de la velocidad  sea nula (máximo de la parábola); y que el alcance horizontal
sea nula (máximo de la parábola); y que el alcance horizontal  ocurrirá cuando el cuerpo retorne al suelo, en
ocurrirá cuando el cuerpo retorne al suelo, en 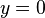 (donde la parábola corta al eje
(donde la parábola corta al eje  ).
).
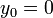 (no así en la animación respectiva). En esa figura también se observa que la altura máxima en la trayectoria parabólica se producirá en H, cuando la componente vertical de la velocidad
(no así en la animación respectiva). En esa figura también se observa que la altura máxima en la trayectoria parabólica se producirá en H, cuando la componente vertical de la velocidad  sea nula (máximo de la parábola); y que el alcance horizontal
sea nula (máximo de la parábola); y que el alcance horizontal  ocurrirá cuando el cuerpo retorne al suelo, en
ocurrirá cuando el cuerpo retorne al suelo, en 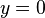 (donde la parábola corta al eje
(donde la parábola corta al eje  ).
).[editar]Movimiento circular uniforme
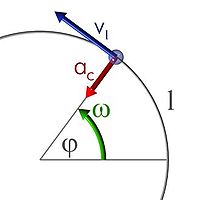
Se caracteriza por tener una velocidad angular constante por lo que la aceleración angular es nula. La velocidad lineal de la partícula no varía en módulo, pero sí en dirección. La aceleración tangencial es nula; pero existe aceleración centrípeta (la aceleración normal), que es causante del cambio de dirección.
Matemáticamente, la velocidad angular se expresa como:
donde 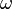 es la velocidad angular (constante),
es la velocidad angular (constante),  es la variación del ángulo barrido por la partícula y
es la variación del ángulo barrido por la partícula y 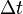 es la variación del tiempo.
es la variación del tiempo.
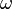 es la velocidad angular (constante),
es la velocidad angular (constante),  es la variación del ángulo barrido por la partícula y
es la variación del ángulo barrido por la partícula y 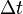 es la variación del tiempo.
es la variación del tiempo.
El ángulo recorrido en un intervalo de tiempo es:
[editar]Movimiento circular uniformemente acelerado
En este movimiento, la velocidad angular varía linealmente respecto del tiempo, por estar sometido el móvil a una aceleración angular constante. Las ecuaciones de movimiento son análogas a las del rectilíneo uniformemente acelerado, pero usando ángulos en vez de distancias:
siendo  la aceleración angular constante.
la aceleración angular constante.
 la aceleración angular constante.
la aceleración angular constante.

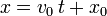


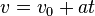





 , de
, de  .
.

 que sigue una trayectoria parabólica.
que sigue una trayectoria parabólica.
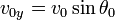
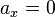







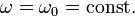
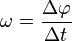
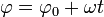

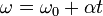

Bonito:D
ResponderEliminar